[See
ref 1, ref 3]
This most amazing symmetry between the numbers of any pair of mutually reverse complementary mono-,di-, tri,...,nucleotides of a DNA duplex of one and the same
strand has many names. We adopt here interchangeably the terms 'intra-strand symmetry' or 'Chargaff's second parity rule'. There is also a 'Chargaff's first parity rule. They are
formulated as follows:
CHARGAFF'S RULES.
Chargaff’s FIRST Parity Rule nucleotides for mono- and oligo-nucleotides:
“The numbers of mono-, di-, tri-,...,nucleotides on one strand of a natural duplex DNA molecule are equal to the numbers of their reverse
complements on the other.”
EXPLANATION: The explanation for this rule is base-pairing.
Surprisingly, indeed, very surprisingly, the same is true for EACH OF THE SINGLE STRANDS of the duplex.
Chargaff’s SECOND Parity Rule nucleotides for mono- and oligo-nucleotides:
“The numbers of mono-, di-, tri-,...,nucleotides on one strand of a natural duplex DNA molecule (>100 kb) are equal to the numbers of their reverse complements on one and the SAME STRAND.”
EXPLANATION: NOT base pairing, but what?
The conundrum.
How is the second rule possible? There cannot be a mechanism that is able to count along a DNA strand how many e.g. TTCA's exist and adjust the number of TGAA's
accordingly.
As will be shown below, this rule is almost universally valid.
Therefore, the explanation for this rule cannot be base-pairing because the bases of the either strand are very rarely paired with each other along the same strand.
The very idea of the double helix demands that they are practically always paired with the bases of the opposite strand. Furthermore, it is easy to construct countless duplex DNA sequences that base-pair and,
thus, fulfil the first rule completely. Yet, they do not fulfil the second. Therefore, I will present another explanation that derives the universal validity of the second rule from the
universal incidence of inversions and inverted transpositions.
Before answering the question let us describe a quantitative way to test this claim. And while we are at it let us reformulate Chargaff's second parity rule.
The reason is that it is a bit arbitrary, to call e.g. ACTG a group of bases and CAGT its reverse complement. Why not the
other way round? Here is how one can avoid characterizing an oligo-nucleotide by the ambiguous term 'reverse complement' in the formulation of the second rule. This
formulation will permit a very simple quantitation of its valididty.
The quantitation of the validity of the rule.
Consider the following example (Click here to display it) of tetra nucleotides that shows both strand of a duplex and highlights corresponding groups of 4 bases.
If W1 represents the number of TTCA's on the Watson-strand then, due to base pairing, there will be exactly C1 = W1
TGAA's on the Crick-strand.
(PLEASE NOTE THAT BASES ARE READ FROM LEFT TO RIGHT ON THE WATSON-STRAND AND RIGHT TO LEFT ON THE CRICK-STRAND)
If Chargaff's second parity rule holds, then there will also be W2 = W1 TGAA's on the Watson-strand and,
consequenctly, there will be C2 = W2 reverse complements TTCA's on the Crick-strand.
So, if Chargaff's second rule holds, then the Watson- and the Crick-strands will have the same number W1 = C2 of TTCA's (and likewise all other
tetra-nucleotides), regardless whether they are considered tetra-nucleotides, or reverse complements of some other tetra-nucleotide.
Hence, we may reformulate
Chargaff’s SECOND Parity Rule:
“The numbers of mono-, di-, tri-,...,nucleotides on one strand of a natural DNA duplex (>100 kb) are the same as on the other.”
In this presentation we will focus on triplets. If they obey Chargaff's second parity rule it will be more amazing than in the case of single bases. Furthermore,
triplets also serve as codons and thus the rule has some bearing on both-strand coding.
Therefore, in order to test the validity of Chargaff's second parity rule, one has to count how often each of the 64 possible triplets occurs on the Watson-strand,
and then do the same for the Crick-strand.
If the rule hold, then the count should be the same. The latter can be tested by a simple correlation plot as in Figure 1.

Fig.1. Method of testing the validity of the intra-strand symmetry using a correlation plot between the
triplet frequencies of the Watson- (abscissa) and Crick-strands (ordinate) of the same sequence.
If a sequence complies completely, the plot generates a straight diagonal line with a correlation
coefficient of cWC = 1.0 . In the above case the genome complies quite well because its correlation coefficient
cWC = 0.9994.
It is obvious from the resulting straight line that the 2 kinds of counts are quite similar. How similar they are can be measured quantitatively by the correlation coefficient cWC
between them. In the following we will use this measure to test how universally true the rule is.
The evidence for the almost universal validity.
Using a computer program that I had written for this purpose I tested genomes whose size was less that 8 Mb by direct analysis.
If a genome was larger, it was cut into sizes of 8 Mb and their triplet profile was measured individually.
Based on the analysis of more than 500 genome segments of 8 Mb size or smaller, the triplet frequencies of their Watson- and
Crick-strands were virtually identical. Only a subset of mitochondrial genomes violated this identity (see below). In all other
cases the standard deviation of the differences between the frequencies of all triplets on the Watson-strand and the corresponding frequencies on
the Crick-strand was <2%. Correspondingly, the correlation coefficients between the Watson and Crick strands cWC were found to be close to unity.
The high degree of compliance is not a matter of randomness of the genome sequences tested. By the very definition of randomness,
all triplets of a random nucleotide sequence must occur with the same frequency. Therefore, its correlation plot must degenerate into a single point
on the diagonal and the correlation coefficient becomes cWC = 0/0 (indeterminate). The triplet profiles of all 500+ tested genome segments were
markedly different from such a constant function demonstrating that none of the natural occurring genomes were random sequences.
More specifically, the correlation coefficients cWC for each 8 Mb large segment of the entire human chromosome 1 were close to a
value of 1.0 (Fig.2a), although in certain locations one or several 'spikes' of the correlation coefficient appeared to drop as low as 0.994.
Similarly, I tested each human chromosome individually and found that each complied with the symmetry rule along its entire length
(Fig 2b). Individual chromosomes of other organisms including Chimpanzee, Dog, Mouse, Zebrafish, D. melanogaster, C.elegans, Maize,
Yeast (S. cervisiae), and B.subtilis showed similar results (Fig. 2c).

Fig.2.Almost universal validity of the intra-strand symmetry ('Chargaff's second parity rule') as applied to triplets. The correlation
coefficient cWC is shown to vary only on the third decimal point. (Ordinate: correlation coefficient cWC;
Abscissa: location along the chromosome)
a. The correlation coefficients for each of the 8 Mb large segments along the entire length of human chromosome 1.
b. Average correlation coefficients cWC for all human chromosomes averaged over 8 Mb segments along their entire length.
c. The correlation coefficients of arbitrarily selected entire chromosomes of various species ranging from primates to bacteria.
Compliance with Chargaff's second parity rule as a function of sequence length.
The shorter the genome segment was, the more the correlation coefficient cWC deviated from the ideal value of 1.0000. In the case of
Human chromosome 1 the correlation coefficient cWC =0.995 was constant for sequences ranging in size from 10 Mb to 1 Mb. Between 1 Mb and 100 kb
cWC decreased to a value of 0.93. Between 100 kb and 10 kb cWC fluctuated considerably, and at sizes below 10 kb, the
value of cWC decreased quite rapidly (Fig.3a).
Violations of Chargaff's second parity rule by many mitochondrial genomes
In the course of the above tests it appeared that human mitochondrial genomes violated the symmetry rule. In order to test to
what degree the same was true for all mitochondria I tested 51 mitochondrial genomes that belonged to a wide range of organisms.
They included fungi, amoebae, invertebrates, insects, plants, slime mold, arthropods, and vertebrates such as amphibians,
reptiles, marsupials, and mammals. They ranged in size between 14 kb (Limulus polyphemus) and 490 kb (Oryza sativa (rice)).
Seventeen mitochondrial genomes were found to comply accurately with Chargaff's second parity rule. Similar to the human
mitochondrial genomes, however, 34 other mitochondrial genomes were found to violate Chargaff's second parity rule to various
degrees (Fig. 3b).
There is possibly an evolutionary explanation for the violation by several mitochondrial genomes, because most of the
violators belonged to recent vertebrates.
Did some of the mitochondrial genomes violate the symmetry rule because mitochondria are not autonomous organisms? In order
to examine this question, I also evaluated 42 chloroplast genomes which are not autonomous organisms, as well. The examples
included those of seed plants as examples of the highest evolved plants, and of non-seed plants such as protists, algae, mosses,
and ferns, ranging in size between 105 kb and 201 kb (average: 150 kb (std.dev 21 kb)). Despite their dependence on host cells,
42 chloroplast genomes complied quite accurately with Chargaff's second parity rule. Their average degree of compliance
was cWC = 0.990 (std.dev. 0.017) which was considerably better than a value of cWC = 0.93 than one would expect based on
their average size of 150 kb.
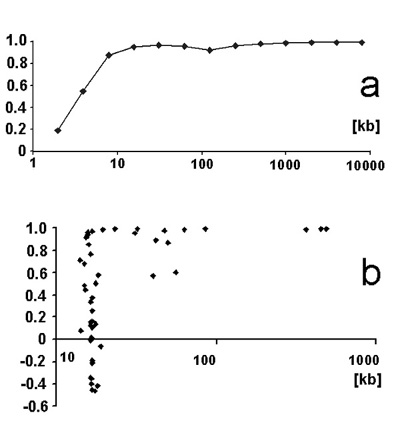
Fig.3. Role of genome size in the validity of the intra-strand symmetry ('Chargaff's second parity rule').(Abscissa: correlation
coefficients cWC;
Ordinate : genome size)
a.Correlation coefficients cWC of different size segments that include the 5' end of human chromosome 1.
b.Violation of the symmetry rule by mitochondrial genomes and lack of a size correlation between the correlation coefficients cWC of 51 mitochondrial genomes and their genome sizes.
An explanation.
The asymptotic equalization of strand properties through the actions of countless inversions and inverted transposions.
Of course, there is no genomic mechanism that is able to count along a DNA strand how many triplet of each kind exist and adjust the
number of the reverse
complementary triplets of each kind, accordingly.
The explanation for this remarkable itra-strand symmetry has to be sought elsewhere.
I propose a mechanism that is based on inversions and inverted transpositions. These genome variations insert sections of a chromosome
in reverse order in their original location (inversions) or somewhere else (inverted transpositions).
To be sure, the inversion of the base sequence itself would have no significance for validity of the rules, if it were not for the
necessity to swap strands. In other words, the particular strand of such an inversion that was part of a Watson-strand before its
excision has to be inserted into the Crick-strand and vice versa. As will be shown below, this action must equalize in an asymptotic
fashion the base composition and oligo-nucleotide composition of the genome in question.
Assume e.g. that initially the number of G's is much larger than the number of C's on a Watson strand. Therefore, due to base
pairing the Crick-strand contains correspondingly more C's than G's. Due to its strand swapping effect, every randomly located
transposition/inversion must carry some of the supernumerary G's from the Watson-strand to the Crick strand while, at the same
time, it carries some of the supernumerary C's from the Crick-strand to the Watson strand. The result is an ongoing equalization
of the numbers of G's with C's on both strands. In a similar way, the mechanism equalizes the numbers of A's and T's on each strand.
In contrast, it does not equalize the numbers of G's with A's, G's with T's, etc. because they are not paired with each other
in the inverted segments.
The process is effectively irreversible, because the equalization caused by a certain transposition/inversion can only be undone
by reversing it exactly immediately afterwards. Such an exact reversion, however, is extremely unlikely to occur in the random fashion,
the transposition/inversions are assumed to happen.
The process is also self-stabilizing, because once a genome complies with Chargaff's second parity rules, the described mechanism
maintains the compliance forever. In this case both strands of the inverted segment has - on average - equal numbers of complementary
nucleotides, and thus it brings as many nucleotides into a strand as it takes away from it. Thus compliance is a stable end state of
genomes that are subjected to the process described by the transposition/inversion hypothesis.
The principle effect of such large numbers of inversions/transpositions on strand symmetry is illustrated in Figure 4. Each duplex
DNA is depicted as a pair of straight ribbons labeled as 'Watson' or 'Crick'. The four nucleotides are represented by shades of gray
that color the various segments of the ribbons (Fig.4a). For the sake of simplicity I assumed that all inverted transposons had a
constant size (see frames in Fig.4b, 4c, labeled 'inv/tp').
Visual illustration of the increasing equalization
The illustration starts with the simplest possible situation of a duplex consisting of a poly-A strand and its complementary poly-T
strand (Fig.4b, '0'). At this stage the Watson-strand contains only A's, AA's and AAA's, but no T's, TT's or TTT's. Likewise, the
Crick-strand has only T's, TT's, and TTT's, but no A's, AA's or AAA's. Obviously, there is no symmetry between these strands.
The situation changes after the first inverted transposition has carried some T's to the Watson-strand while carrying an equal
number of A's to the Crick-strand (Fig. 4b, '1', '2'). At this point not only do the complementary nucleotides appear on either
strand. They also generate some mixed triplets such as ATT, TTA, AAT, and TAA for the first time on both strands. As the process
continues and the number of randomly placed inverted transpositions increases, the distributions of A's, T's, and their
corresponding doublets and triplets become increasingly the same. (Please note, that the sequences do not become the same,
but only their mono-, di,-, tri-,…nucleotide distributions do.)
A more detailed analysis shows that the equalization of the
nucleotide distributions grows exponentially with the number of inversions/transpositions.
Similarly, if the initial duplex contains all four nucleotides in some arbitrary ratio, the strands become exponentially more
symmetrical with the increasing number of inversions/transpositions. An example is shown in Fig.4c.
Animated versions of Figures 4b and 4c are shown in Figures 4d and 4e. Note that the increasing numbers of inversions and inverted
transpositions not only equalize the overall base counts on either strand but the sub-segments of either strands that still violate the symmetry rule became shorter and shorter. In other words,
the model also explains the result shown in Fig. 3a,namely that the larger the DNA segment, the better the symmetry is fulfilled.

Fig.4. Illustration of the effect of large numbers of inversions/transpositions on the strand symmetry.
Each duplex DNA is depicted as a pair of straight ribbons labeled as 'Watson' or 'Crick'. For the sake of simplicity we
assume that all inverted transposons have a constant size (see frames in panels b and c, labeled 'inv/tp').
a. Color coding of the 4 nucleotides by shades of gray that color the various segments of the ribbons.
b. Equalization of the numbers of A's and T's in the case of a duplex consisting of a poly-A strand and its complementary
poly-T strand ('0'). Obviously, initially there is no symmetry between these strands. As the number of randomly placed inversion
increases they carry increasing numbers of T's to the Watson-strand while carrying an equal number of A's to the Crick-strand
panel b, '1', '2'). They also generate some mixed triplets such as ATT, TTA, AAT, and TAA for the first time on both strands.
As the process continues and the number of randomly placed inverted transpositions increases, the distributions of A's, T's,
and their corresponding doublets and triplets become increasingly the same. A more detailed analysis shows that the equalization
of the nucleotide distributions grows exponentially with the number of inversions/transpositions.
c. Similarly, if the initial duplex contains all 4 nucleotides in some arbitrary ratio, the strands become exponentially
more symmetrical with the increasing number of inversions/transpositions as indicated by the numbers at each duplex.

Fig.4d. Animated version of Figure 4b.Starting with the extremely asymmetrical situation of predominantly A's on one strand and correspondingly predominantly T's on the other, the increasing
numbers of inversions and inverted transpositions asymptotically equalize the numbers of the 2 bases on either strand (see numbers above the display), but also
decrease the size of sub-segments of the duplex that still violate the symmetry rule.(cf. Fig.3a)

Fig.4e. Animated version of Figure 4c.Starting with the extremely asymmetrical situation of predominantly A's and C's on one strand and correspondingly predominantly T's and G's on the other, the increasing
numbers of inversions and inverted transpositions asymptotically equalize the numbers of the 2 bases on either strand (see numbers above the display), but also
decrease the size of sub-segments of the duplex that still violate the symmetry rule.(cf. Fig.3a)
Mathematical illustration of the increasing equalization
It is easy to express the above illustration mathematically and solve the resulting equations. (See ref 1). Figure 5 shows
the example of the asymptotic increase of compliance and the concommitant equalization of the numbers of C's and G's with the number of inversions/inverted transpositions. The asymptotic value of
the bases duplets, triplets, etc. is always the arithmetic mean between the 2 starting values on the Watson-strand and the Crick-strand:
vinfinity = ( vW + vC)/2.
(cf the progression of numbers of bases in Fig. 4d and 4d).
mean of the starting values.
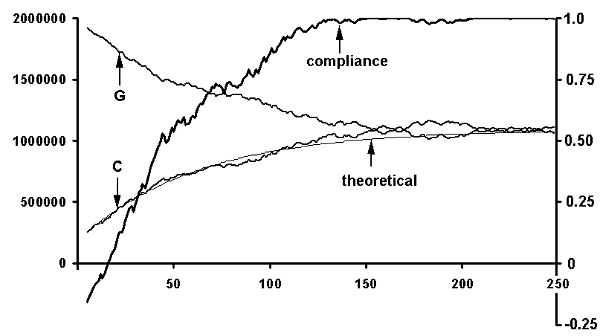
Fig.5. Simulation of the convergence of a non-compliant genome to a compliant one by a recursive series of
transposition/inversions. (Abscissa: number of rounds of transposition/inversions; left ordinate: number of G's or
C's on the resulting Watson strand; right ordinate: degree of compliance of the resulting genome with Chargaff's second parity rule
expressed as correlation coefficient cWC )
The thick line labeled 'compliance' depicts the simulated genome's degree of compliance with the
tinbtr-strand symmetry as a function of rounds of transposition/inversions. The thinner lines labeled 'G' and 'C' depict the
convergence of the numbers of the corresponding nucleotides during the same process. The thin line labeled 'theoretical'
depicts the theoretical curve of convergence. Note: This curve is not fitted to the simulation,
but merely uses the same value of (segment size/genome size). For the sake of graphic presentation the simulation assumed
a large ratio of (size of average inverted segment)/(size of whole genome) of 0.008. It appears that the theoretical
description matches quite accurately the exponential convergence of a non-compliant genome to a compliant one.
Significance for the "functional anarchy" of genomes:
Equalisation of physical properties of the strands
The 2 strands of a duplex have, of course, very different sequences, both locally and globally. Yet, the almost universal validity
of the intra-strand symmetry means that both strands have identical statistical distributions ( see the re-formulation of Chargaff's second parity rule) and, thus, identical physical properties. If, as suggested here, this
amazing symmetry was created by countless 'reckless' inversions and inverted transpositions, their kind of anarchy also equalized and, thus,
increased the physical stability of the 2 strands. At the same time it may have decreased their vulnerability which may stem from
highly special configurations of bases present on only one of the strands. Their equalized physical properties may also have aided repair
mechanisms and facilitated chromatin formation as well as horizontal gene transfer and, thus may have accelerated evolution.
Continuation of the process in perpetuity
The proposed mechanism also suggests that the valitdity of Chargaff's second parity rule describes a work in progress. As is obvious
from Figure 4, a small number of large inversions can quickly equalize the overall properties of
the strands (e.g. Fig. 4b; label '2'), but at that stage small sub-sections of the sequences are far from being equalized. It takes many more
inversions/inverted transpositions before even small segments have reached a state of intra-strand symmetry (see Fig.4 c; label '10000'). Actually,
the job is never finished and, indeed, Figure 3a, shows that the human genome is equalized, in general,
only down to sequence portions of 100 kb and larger. Smaller stretches are still violating the rule: the work of the inversions/inverted transpositions is yet to be continued.
Invariance against the major other mechanisms of variation
Even if it is true that inversions and inverted transpositions created the intra-strand symmetry, why did the many other 'anarchy wreaking' mechanisms of mutation not
destroy it? It will be helpful for the discussion to describe the reformulated version of Chargaff's second parity rule
by the simple formula:
NW(Tn) = NC(Tn)
where NW(or C)(Tn) stand for the counts of each of the 64 triplets Tn on the Watson (or Crick) strand.
(NOTE that the formulation uses the actual triplet counts, not the normalized counts of a distribution!)
Now, et us look at some of the major mechanisms of mutation (variation) and test whether they are able to destroy the strand symmetry. It will be quite obvious that they do not.
Concatenation and insertion:
If 2 sequences S1 and S2 comply with the rule, so does their concatenation or the insertion of one into the other because the frequency counts of the triplet distributions are additive, i.e.:
If NW(Tn)1 = NC(Tn)1 and NW(Tn)2 = NC(Tn)2 then
NW(Tn)1 + NW(Tn)2 = NC(Tn)1 + NC(Tn)2.
Deletion:
If a sequences S1 complies with the rule, so does each sufficiently large subsection S2. Therefore,deleting S2 from S1 leave the compliance intact, because
If NW(Tn)1 = NC(Tn)1 and NW(Tn)2 = NC(Tn)2 then
NW(Tn)1 - NW(Tn)2 = NC(Tn)1 - NC(Tn)2.
Recombination:
If both alleles comply with the rule, then the exchange of a segments cannot change the equality of counts between the Watson- and Crick-strands.
Transposition:
The numbers NW(Tn)and NC(Tn) of each triplet Tn are independent of their location in the sequence.
Therefore, moving them around does not change the counts on either strand and,
thus, conserves the compliance.
Base substitution:
Base substitution have to potential to change the triplet balance between the 2 strands. However, in reality the number
of point mutations is miniscule compared to the size of most genomes. Therefore, the imbalances caused by point mutations fall within the natural range of variations of the numbers NW(Tn)and NC(Tn).
Thus it seems that all the other, major 'anarchy-wreaking' mechanisms of variation leave the strand symmetry intact. Of course, it is possible to invent special kinds of mutations that would cause
violations of the strand symmetry, but it seems that none of them exists in reality. Otherwise, it would be impossible to understand the almost universal validity of Chargaff's second parity rule.
Based on this unversality, one may even go so far as to predict that if there are presently unknown major mechanism of variation, they may be discovered by searching for mutational mechanisms that leave the strand
symmetry intact.
Is there a selective advantage?
Considering the almost universal validity of Chargaff's second parity rule, there seems to be no selective advantage in obeying it. Every competitor obeys it, too. Of course, violating it
could mean a severe disadvantage. For example, the almost universal use of L-amino acids represents no particular selective advantage, whereas the need
to use D-amino acids would pose the severe problem for an organism here on Earth to find food. However, the evolutionary success of so many mitochondrial genomes
seems to suggest that there is no disadvantage associated with the violation of the rule, either, although this example may point to the need to obey the rule, if the
genome is to exist autonomously inside its own organism.
Therefore, until further insights come along, we may consider the compliance with the symmetry rule as an evolutionary neutral, though inevitable side effect of numerous transpositions, specifically
the cases among them where the transposons invert and swap strands. The transposition themselves, of course, confer a major selective advantages because, as Barbara McClintock (1902-1992) pointed out in her Nobel speech, they offer genomes the possibility to respond to unforseeable "genome shocks".







